RMS Power vs. Average Power

Answer: It depends on how you define rms power. You do not want to calculate the rms value of the ac power waveform. This produces a result that is not physically meaningful. You do use the rms values of voltage and/or current to calculate average power, which does produce meaningful results. Discussion How much power is dissipated when a 1 V rms sinusoidal voltage is placed across a 1 Ω resistor? This is well understood1 and there is no controversy here. Now, let’s see how this compares with the value from an rms power calculation. Figure 1 shows a graph of a 1 V rms sinusoid. 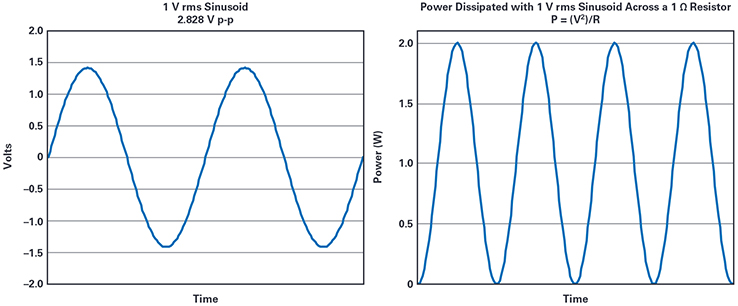The peak-to-peak value is 1 V rms × 2 √2 = 2.828 V, swinging from +1.414 V to –1.414 V.2 Figure 1. Graph of a 1 V rms sinusoid. / Figure 2. Graph of the power dissipated by a 1 V rms sinusoid across a 1 Ω resistor. Figure 2 is a graph of the power dissipated by this 1 V rms sinusoid across a 1 Ω resistor (P = V2/R) that shows:

• The instantaneous power curve has an offset of 1 W and swings from 0 W to 2 W.
• The rms value of this power waveform is 1.225 W.

One method of calculating this number is Equation 2,3: This can be verified by using a more detailed formula4 in MATLAB® or Excel.

• The average value of this power waveform is 1 W. This is obvious from inspection; the waveform swings symmetrically above and below 1 V. The same value results from calculating the numerical average of the waveform datapoints.
• The average power value matches the power calculated using rms voltage.

The power dissipated by a sinusoidal 1 V rms across a 1 Ω resistor is 1 W, not 1.225 W. Thus, it is the average power that produces the correct value, and thus it is average power that has physical significance. The rms power (as defined here) has no obvious useful meaning (no obvious physical/electrical significance), other than being a quantity that can be calculated as an exercise. It is a trivial exercise to perform the same analysis using a 1 A rms sinusoidal current through a 1 Ω resistor. The result is the same. Power supplies for integrated circuits (ICs) are generally dc, so rms power is not an issue for IC power. For dc, average and rms are the same value as dc. The importance of using average power, as opposed to rms power as defined in this document, applies to power associated with time-varying voltage and current—that is, noise, RF signals, and oscillators. Use rms voltage and/or rms current to calculate average power, resulting in meaningful power values. References

1. Power dissipated from voltage across a resistor is a fundamental relation that is easily derived from Ohm’s law (V = IR) and the fundamental definitions of voltage (energy/unit of charge) and current (unit of charge/time). Voltage × current = energy/time = power
2. The peak-to-peak amplitude of a sinusoid is the rms value multiplied by 2√2. For a sinusoidal voltage, V p-p = V rms × 2√2, where V p-p is the peak-to-peak voltage and V rms is the rms voltage. This is a well-known relation that is documented in countless text books, as well as here: en.wikipedia.org/wiki/Root_mean_square.
3. This is adapted from the rms value calculated from a constant dc offset value plus a separate rms ac value and in the application note “Make Better AC RMS Measurements with Your Digital Multimeter” by Keysight.
4. The standard textbook definition is one example of a more detailed formula.

---

About the Author: Doug Ito is an applications engineer for the High Speed ADC team at © Analog Devices, Inc., San Diego, California. He earned a bachelor’s degree in electrical engineering from San Diego State University. Doug is a member of ADI’s EngineerZone® High Speed ADC Support Community. He can be reached at douglas.ito@analog.com.